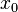Loi log-Cauchy

En théorie des probabilités et en statistique, la loi log-Cauchy est la loi de probabilité d'une variable aléatoire dont le logarithme suit une loi de Cauchy. Si X suit une loi de Cauchy, alors ${\displaystyle Y=\exp(X)}$ est de loi log-Cauchy ; similairement, si Y suit une loi log-Cauchy, alors ${\displaystyle X=\ln(Y)}$ est de loi de Cauchy.

Cette loi dépend de deux paramètres ${\displaystyle \mu }$ et ${\displaystyle \sigma }$. Si une variable X suit une loi log-Cauchy, on notera ${\displaystyle X\sim LC(\mu ,\sigma )}$.

Caractérisation

Densité de probabilité

La densité de probabilité de la loi log-Cauchy est donnée par :

${\displaystyle {\begin{aligned}f(x;\mu ,\sigma )&={\begin{cases}{\frac {1}{x\pi \sigma \left[1 \left({\frac {\ln x-\mu }{\sigma }}\right)^{2}\right]}}&{\text{ si }}x>0\\0&{\text{ sinon}}\end{cases}}\\&={1 \over x\pi }\left[{\sigma \over (\ln x-\mu )^{2} \sigma ^{2}}\right]{\textbf {1}}_{\{x>0\}}\end{aligned}}}$

où ${\displaystyle \mu }$ est un nombre réel et ${\displaystyle \sigma >0}$^,. Si ${\displaystyle \sigma }$ est connu, le paramètre d'échelle est ${\displaystyle e^{\mu }}$. Les paramètres ${\displaystyle \mu }$ et ${\displaystyle \sigma }$ correspondent respectivement aux paramètres de position et d'échelle de la loi de Cauchy associée^,. Certains auteurs définissent ${\displaystyle \mu }$ et ${\displaystyle \sigma }$ comme, respectivement, les paramètres de position et d'échelle de la loi log-Cauchy.

Pour ${\displaystyle \mu =0}$ et ${\displaystyle \sigma =1}$, la loi log-Cauchy est associée à la loi de Cauchy standard, la densité de probabilité est alors réduite à :

${\displaystyle f(x;0,1)={\begin{cases}{\frac {1}{x\pi (1 (\ln x)^{2})}}&{\text{ si }}x>0\\0&{\text{ sinon.}}\end{cases}}}$

Fonction de répartition

La fonction de répartition pour ${\displaystyle \mu =0}$ et ${\displaystyle \sigma =1}$ est :

${\displaystyle F(x;0,1)={\begin{cases}{\frac {1}{2}} {\frac {1}{\pi }}\arctan(\ln x)&{\text{ si }}x>0\\0&{\text{ sinon.}}\end{cases}}}$

Fonction de survie

La fonction de survie pour ${\displaystyle \mu =0}$ et ${\displaystyle \sigma =1}$ est :

${\displaystyle S(x;0,1)={\begin{cases}{\frac {1}{2}}-{\frac {1}{\pi }}\arctan(\ln x)&{\text{ si }}x>0\\1&{\text{ sinon.}}\end{cases}}}$

Taux de défaillance

Le taux de défaillance pour ${\displaystyle \mu =0}$ et ${\displaystyle \sigma =1}$ est :

${\displaystyle \lambda (x;0,1)=\left({\frac {1}{x\pi \left(1 \left(\ln x\right)^{2}\right)}}\left({\frac {1}{2}}-{\frac {1}{\pi }}\arctan(\ln x)\right)\right)^{-1},\ \ x>0}$

Le taux de hasard décroit au début et sur la dernière partie du support de la densité, mais il peut exister un intervalle sur lequel le taux de hasard croît.

Propriétés

La loi log-Cauchy est un exemple de loi à queue lourde. Certains auteurs la considère comme une loi à « queue super-lourde », car elle possède une queue plus lourde que celles de type de la distribution de Pareto, c'est-à-dire qu'elle a une décroissance logarithmique^,. Comme avec la loi de Cauchy, aucun des moments (non triviaux) de la loi log-Cauchy n'est fini. La moyenne et l'écart-type étant des moments, ils ne sont pas définis pour la loi log-Cauchy^,.

La loi log-Cauchy est infiniment divisible pour certains paramètres. Comme les lois log-normale, log-Student et de Weibull, la loi log-Cauchy est un cas particulier de loi bêta généralisée du second type^,. La loi log-Cauchy est en fait un cas particulier de la loi log-Student, comme la loi de Cauchy est un cas particulier de la loi de Student à un degré de liberté^,.

Puisque la loi de Cauchy est une loi stable, la loi log-Cauchy est une loi log-stable.

Estimation des paramètres

La médiane du logarithme naturel d'un échantillon est un estimateur robuste de ${\displaystyle \mu }$.

Références

• Portail des probabilités et de la statistique